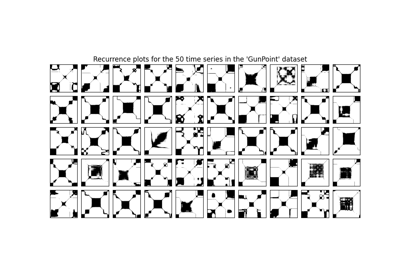
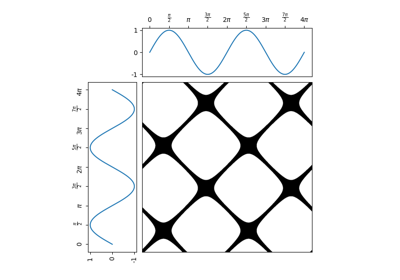
RecurrencePlot

class pyts.image.RecurrencePlot(dimension: int | float = 1, time_delay: int | float = 1, threshold: float | str | None = None, percentage: int | float = 10, flatten: bool = False)

Recurrence Plot.

A recurrence plot is an image representing the distances between trajectories extracted from the original time series.

Parameters:

dimensionint or float (default = 1)

Dimension of the trajectory. If float, it represents a percentage of the size of each time series and must be between 0 and 1.

time_delayint or float (default = 1)

Time gap between two back-to-back points of the trajectory. If float, it represents a percentage of the size of each time series and must be between 0 and 1.

thresholdfloat, ‘point’, ‘distance’ or None (default = None)

Threshold for the minimum distance. If None, the recurrence plots are not binarized. If ‘point’, the threshold is computed such as percentage percents of the points are smaller than the threshold. If ‘distance’, the threshold is computed as the percentage of the maximum distance.

percentageint or float (default = 10)

Percentage of black points if threshold='point' or percentage of maximum distance for threshold if threshold='distance'. Ignored if threshold is a float or None.

flattenbool (default = False)

If True, images are flattened to be one-dimensional.

Notes

Given a time series \((x_1, \ldots, x_n)\), the extracted trajectories are

\[\vec{x}_i = (x_i, x_{i + \tau}, \ldots, x_{i + (m - 1)\tau}), \quad \forall i \in \{1, \ldots, n - (m - 1)\tau \}\]

where \(m\) is the dimension of the trajectories and \(\tau\) is the time_delay. The recurrence plot, denoted \(R\), is the pairwise distance between the trajectories

\[R_{i, j} = \Theta(\varepsilon - \| \vec{x}_i - \vec{x}_j \|), \quad \forall i,j \in \{1, \ldots, n - (m - 1)\tau \}\]

where \(\Theta\) is the Heaviside function and \(\varepsilon\) is the threshold.

References

[1]

J.-P Eckmann, S. Oliffson Kamphorst and D Ruelle, “Recurrence Plots of Dynamical Systems”. Europhysics Letters (1987).

Examples

>>> from pyts.datasets import load_gunpoint
>>> from pyts.image import RecurrencePlot
>>> X, _, _, _ = load_gunpoint(return_X_y=True)
>>> transformer = RecurrencePlot()
>>> X_new = transformer.transform(X)
>>> X_new.shape
(50, 150, 150)

Methods

__init__([dimension, time_delay, threshold, ...])
fit([X, y])	Pass.
fit_transform(X[, y])	Fit to data, then transform it.
get_metadata_routing()	Get metadata routing of this object.
get_params([deep])	Get parameters for this estimator.
set_params(**params)	Set the parameters of this estimator.
transform(X)	Transform each time series into a recurrence plot.

__init__(dimension: int | float = 1, time_delay: int | float = 1, threshold: float | str | None = None, percentage: int | float = 10, flatten: bool = False) → None

fit(X: ArrayLike | None = None, y: ArrayLike | None = None) → Self

Pass.

Parameters:

X

Ignored

y

Ignored

Returns:

selfobject

transform(X: ArrayLike) → NDArray[float64]

Transform each time series into a recurrence plot.

Parameters:

Xarray-like, shape = (n_samples, n_timestamps)

Returns:

X_newarray, shape = (n_samples, image_size, image_size)

Recurrence plots. image_size is the number of trajectories and is equal to n_timestamps - (dimension - 1) * time_delay. If flatten=True, the shape is (n_samples, image_size * image_size).

Examples using pyts.image.RecurrencePlot

Data set of recurrence plots

Data set of recurrence plots

Single recurrence plot

Single recurrence plot

Joint Recurrence Plot

Joint Recurrence Plot