Shapelet Transform

The Shapelet Transform algorithm extracts shapelets from a data set of time series and returns the distances between the shapelets and the time series. A shapelet is defined as a subset of a time series, that is a set of values from consecutive time points. The distance between a shapelet and a time series is defined as the minimum of the distances between this shapelet and all the shapelets of same length extracted from this time series. 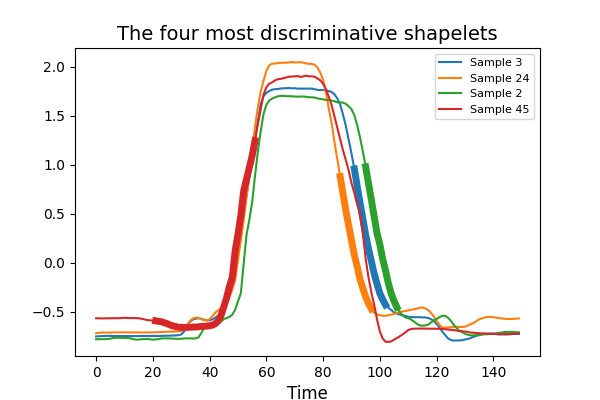The most discriminative shapelets are selected. This example illustrates the transformation of this algorithm and highlights the most discriminative shapelets that have been selected. It is implemented as pyts.transformation.ShapeletTransform.

import numpy as np
import matplotlib.pyplot as plt
from pyts.datasets import load_gunpoint
from pyts.transformation import ShapeletTransform

# Toy dataset
X_train, _, y_train, _ = load_gunpoint(return_X_y=True)

# Shapelet transformation
st = ShapeletTransform(window_sizes=[12, 24, 36, 48],
                       random_state=42, sort=True)
X_new = st.fit_transform(X_train, y_train)

# Visualize the four most discriminative shapelets
plt.figure(figsize=(6, 4))
for i, index in enumerate(st.indices_[:4]):
    idx, start, end = index
    plt.plot(X_train[idx], color='C{}'.format(i),
             label='Sample {}'.format(idx))
    plt.plot(np.arange(start, end), X_train[idx, start:end],
             lw=5, color='C{}'.format(i))

plt.xlabel('Time', fontsize=12)
plt.title('The four most discriminative shapelets', fontsize=14)
plt.legend(loc='best', fontsize=8)
plt.show()