Note
Click here to download the full example code
Bag of Patterns¶
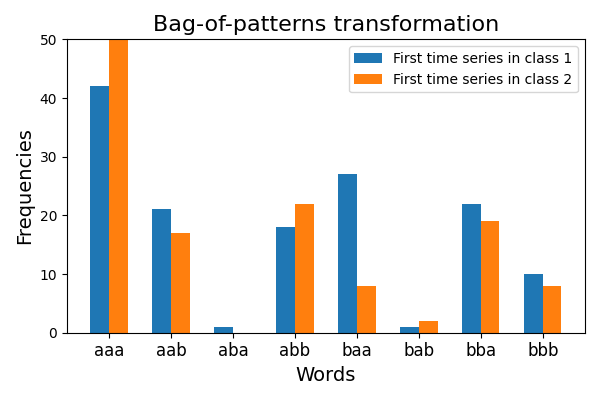
Bag-of-words approaches are common in time series classification. The Bag-of-patterns algorithm uses a sliding window to extract subsequences from the time series and transforms each subsequence into a word using the Piecewise Aggregate Approximation and the Symbolic Aggregate approXimation algorithms. Thus it transforms each time series into a bag of words. Then it derives the frequencies of each word for each time series.
This example illustrates the words and the frequencies of these words that
have been learned by this algorithm. It is implemented as
pyts.transformation.BagOfPatterns.
# Author: Johann Faouzi <johann.faouzi@gmail.com>
# License: BSD-3-Clause
import numpy as np
import matplotlib.pyplot as plt
from pyts.datasets import load_gunpoint
from pyts.transformation import BagOfPatterns
# Toy dataset
X_train, _, y_train, _ = load_gunpoint(return_X_y=True)
# BOSS transformation
bop = BagOfPatterns(window_size=9, word_size=3, n_bins=2,
numerosity_reduction=False, sparse=False)
X_bop = bop.fit_transform(X_train)
# Visualize the transformation for the first time series
plt.figure(figsize=(6, 4))
vocabulary_length = len(bop.vocabulary_)
width = 0.3
plt.bar(np.arange(vocabulary_length) - width / 2, X_bop[y_train == 1][0],
width=width, label='First time series in class 1')
plt.bar(np.arange(vocabulary_length) + width / 2, X_bop[y_train == 2][0],
width=width, label='First time series in class 2')
plt.xticks(np.arange(vocabulary_length),
np.vectorize(bop.vocabulary_.get)(np.arange(X_bop[0].size)),
fontsize=12)
y_max = np.max(np.concatenate([X_bop[y_train == 1][0],
X_bop[y_train == 2][0]]))
plt.xlabel("Words", fontsize=14)
plt.ylabel("Frequencies", fontsize=14)
plt.title("Bag-of-patterns transformation", fontsize=16)
plt.legend(loc='best', fontsize=10)
plt.ylim((0, 50))
plt.tight_layout()
plt.show()
Total running time of the script: ( 0 minutes 0.262 seconds)

