Note
Click here to download the full example code
Transformers¶
Some algorithms make assumptions on the distribution of the data. Therefore it can be useful to transform time series so that they approximatively follow a given distribution. Two transformers are made available:
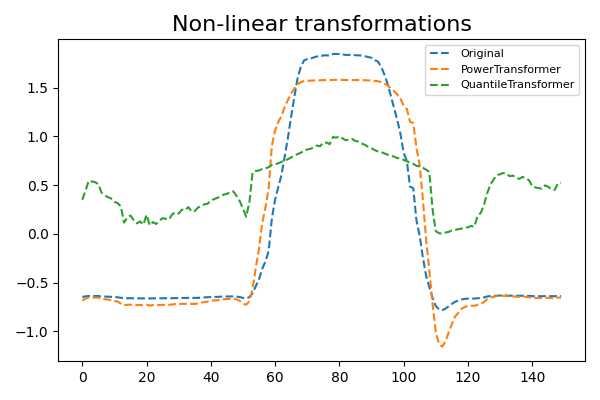
This example illustrates the transformation from both algorithms.
# Author: Johann Faouzi <johann.faouzi@gmail.com>
# License: BSD-3-Clause
import matplotlib.pyplot as plt
from pyts.datasets import load_gunpoint
from pyts.preprocessing import PowerTransformer, QuantileTransformer
X, _, _, _ = load_gunpoint(return_X_y=True)
n_timestamps = X.shape[1]
# Transform the data with different transformation algorithms
X_power = PowerTransformer().transform(X)
X_quantile = QuantileTransformer(n_quantiles=n_timestamps).transform(X)
# Show the results for the first time series
plt.figure(figsize=(6, 4))
plt.plot(X[0], '--', label='Original')
plt.plot(X_power[0], '--', label='PowerTransformer')
plt.plot(X_quantile[0], '--', label='QuantileTransformer')
plt.legend(loc='best', fontsize=8)
plt.title('Non-linear transformations', fontsize=16)
plt.tight_layout()
plt.show()
Total running time of the script: ( 0 minutes 0.343 seconds)

